eastspot.blogg.se - All properties of a rectangle

In order to understand the rectangle better, observe the rectangle given above and relate to the following properties of a rectangle.A rectangle is a quadrilateral with four equal interior angles.The opposite sides of a rectangle are equal and parallel to each other.The interior angle of a rectangle at each vertex measures 90°.The sum of all the interior angles of a rectangle is 360°.All rectangles are parallelograms but all parallelograms are not rectangles.Ī rectangle has four sides with the opposite sides equal to each other and with the adjacent sides meeting at 90°.Since the sides of a rectangle are parallel, it is also called a parallelogram.The length of the diagonal with sides a and b is √( a² + b²). These properties are seen in the two types of rectangles - the Square and the Golden Rectangle.Ī square is a type of rectangle with four equal sides and four equal angles. It is a two-dimensional shape where the interior angles at each vertex are 90°. Along with these properties, the opposite sides of a square are equal and parallel and the diagonals bisect each other at 90°. It can be said that all squares are rectangles but all rectangles cannot be squares. The golden rectangle is a rectangle whose sides are in the golden ratio, that is, (a + b)/a = a/b, where 'a' is the width and (a + b) is the length of the rectangle. In other words, a golden rectangle is a rectangle whose 'length to width ratio' is similar to the golden ratio, 1: (1+⎷ 5)/2. For example, if the length is around 1 foot long then the width will be 1.168 feet long or vice-versa where the Golden Ratio = 1: 1.618. Observe the following figure which shows the golden rectangle and its length and width.Difference Between Square and RectangleįAQs on Properties of Rectangle What are the Properties of a Rectangle?.The basic properties of a rectangle are that its opposite sides are parallel and equal and its interior angles are equal to 90°.

The properties of the diagonal of a rectangle are as follows: What are the Properties of the Diagonals of a Rectangle? Its diagonals are also equal and they bisect each other.

The two diagonals of a rectangle are equal.

The diagonals bisect each other, but not at right angles.

The length of the diagonals can be obtained using the Pythagoras theorem.

Since the diagonals divide the rectangle into two right-angled triangles, they are considered to be the hypotenuse of these triangles.

What is the Difference Between a Square and a Rectangle? Yes, a square is considered as a rectangle because it contains the properties of a rectangle, like, all the four interior angles are 90°, the opposites sides of a square are parallel and equal to each other, and two diagonals of the square are equal and bisect each other. Squares have some additional properties which do not apply to rectangles. A square has four equal sides, whereas, in a rectangle, only the opposite sides are equal.

What are the Various Types of Quadrilaterals other than Rectangles? The diagonals of a square bisect at 90°, but the diagonals of a rectangle do not bisect at 90°. The various types of quadrilaterals other than rectangles are squares, rhombus, kite, parallelogram, and a trapezoid. Why is a Rectangle not a Square?Īlthough many properties of a rectangle are similar to a square but a rectangle is not a square because it does not have all four sides of equal measure.

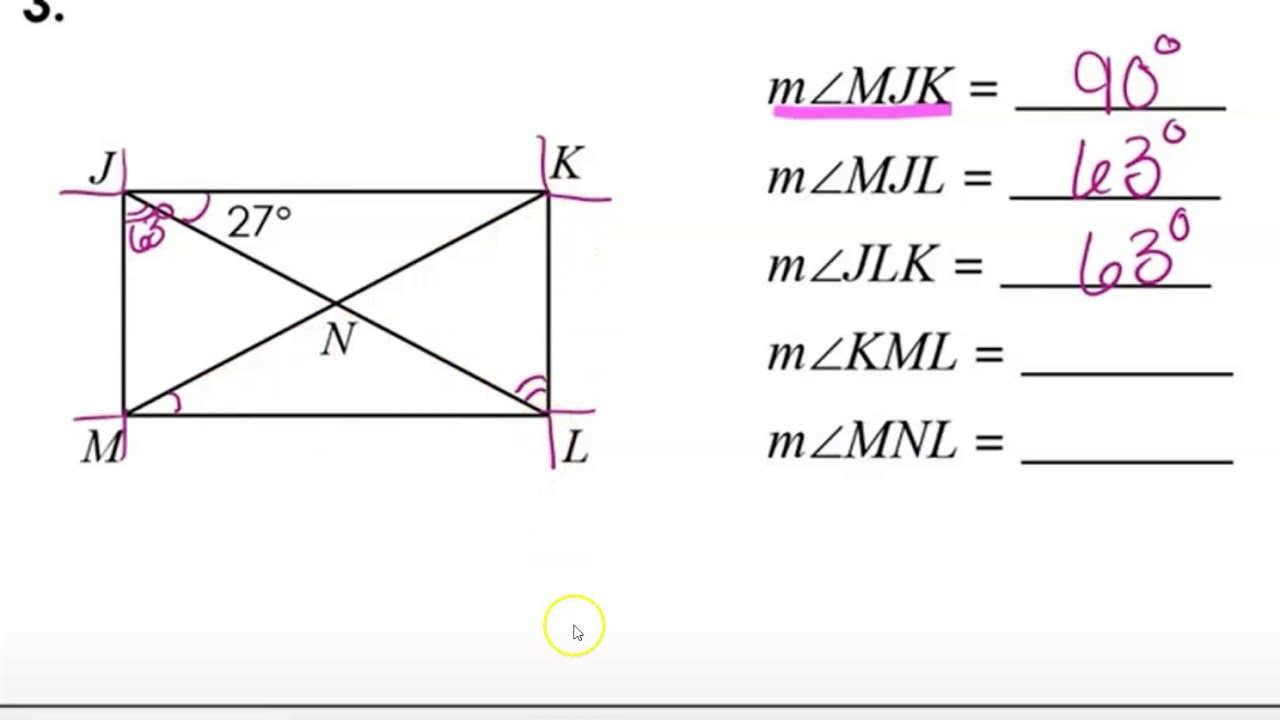
This is the reason that a rectangle is not a square.